原文引自我的力扣题解:针对Floyd 快慢指针算法阶段二的严格数学证明
双指针解法过程
我们使用两个指针,fast 与 slow。它们起始都位于链表的头部。随后,slow 指针每次向后移动一个位置,而 fast指针向后移动两个位置。如果链表中存在环,则 fast指针最终将再次与slow 指针在环中相遇。
证明
从链表头部出发的步数与最后处于的节点编号的函数关系式
对于一个带环的链表,若在环外(包括入环起始位置的节点)的节点数为F,环内节点数目为C,由链表起始位置出发的步数为x,最终指向的节点编号为M,当x<F时,有M = x; 当x>=F时,有F+(x-F)%C,如下图所示。
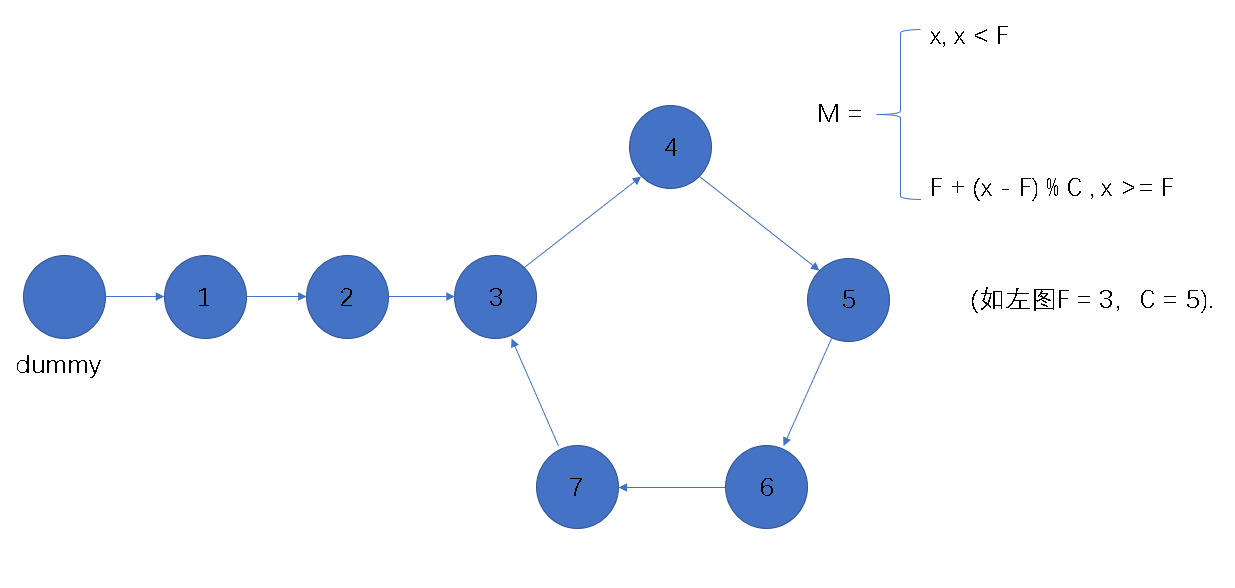
步骤
在第一阶段中,慢指针走了x=n步,快指针走了x=2n步.显然n>=F,则M(n)=F+(n-F)%C,M(2n)=F+(2n-F)%C.
此时快慢指针相遇,则M(n)=M(2n).
即F+(n-F)%C = F+(2n-F)%C
即(n-F)%C = (2n-F)%C
则((2n-F) - (n-F))%C = 0.
求得 n%C=0 (*)
阶段二指针一从链表头部出发,指针二从阶段一相遇处出发,两指针相遇且为入环起始位置,有:
M(n+F) = M(F) = F 成立.
M(F) = F 显然成立.
对于M(n+F) = F,有:
M(n+F) = F+(n+F - F)%C = F + n%C
将(*)代入,M(n+F) = F + n%C = F + 0 = F.
所以阶段二的结论是正确的,证毕.